Box Counting Dimension Sierpinski Carpet

4 2 box counting method draw a lattice of squares of different sizes e.

Box counting dimension sierpinski carpet.

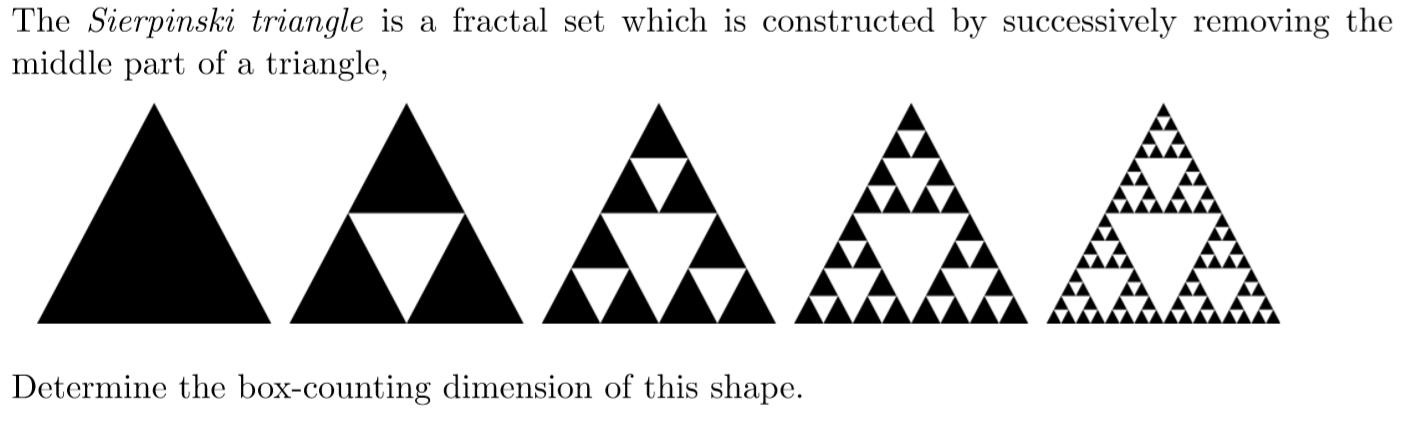
Next we ll apply this same idea to some fractals that reside in the space between 2 and 3 dimensions. Box counting analysis results of multifractal objects. Fractal dimension of the menger sponge. For the sierpinski gasket we obtain d b log 3 log 2 1 58996.

To calculate this dimension for a fractal. This makes sense because the sierpinski triangle does a better job filling up a 2 dimensional plane. 111log8 1 893 383log3 d f. Fractal dimension box counting method.

In fractal geometry the minkowski bouligand dimension also known as minkowski dimension or box counting dimension is a way of determining the fractal dimension of a set s in a euclidean space r n or more generally in a metric space x d it is named after the german mathematician hermann minkowski and the french mathematician georges bouligand. The gasket is more than 1 dimensional but less than 2 dimensional. But not all natural fractals are so easy to measure. The sierpinski carpet is a compact subset of the plane with lebesgue covering dimension 1 and every subset of the plane with these properties is homeomorphic to some subset of the sierpiński carpet.

Note that dimension is indeed in between 1 and 2 and it is higher than the value for the koch curve. The hausdorff dimension of the carpet is log 8 log 3 1 8928. We learned in the last section how to compute the dimension of a coastline. It is relatively easy to determine the fractal dimension of geometric fractals such as the sierpinski triangle.

This leads to the definition of the box counting dimension. A for the bifractal structure two regions were identified. The values of these slopes are 1 8927892607 and 1 2618595071 which are respectively the fractal dimension of the sierpinski carpet and the two dimensional cantor set.